The WSRT array

The Westerbork Synthesis Radio Telescope is a radio interferometer with 14 parabolic dishes. The array is built along an accurately measured East-West line and all interferometer baselines are at right angles to the Earths rotation axis. Any baseline can therefore be specified by the rectangular coordinates of the one antenna relative to the other in a plane perpendicular to the Earth axis. The and coordinates are measured in units of one wavelength at the centre frequency of the observed frequency band and the and directions are fixed in space. At each given point in time every baseline produces a measurement in the plane. As the Earth rotates, every baseline traces an ellipse in this plane.

Since an interferometer has a limited number of telescopes and therefore a limited number of baselines, the plane is not sampled completely. Not sampled points are set to zero in order to calculate the Fourier Transform which gives the radio brightness distribution over the field of view, i.e. the region within the main lobe of the antenna power pattern .

The shape of the synthesized beam in the coordinate system is independent of the direction in the sky. In angular direction, however, the beam is extended in declination by a factor of . This is obvious also from the fact that the measured area is circular only when viewed from the North celestial pole and becomes elliptical in the ratio when seen in projection from other declinations.

The finite number of measured tracks results in a synthesized pattern, in which the central maximum is accompanied by a set of concentric grating circles. Their radii in the coordinate system are where is an integer and is the regular interval between the measured tracks in wavelengths. In angular terms these grating rings are ellipses with semi-axes and radians in the right ascension and declination directions, respectively. The amplitude of the grating ring is inversely proportional to the square root of its radius. 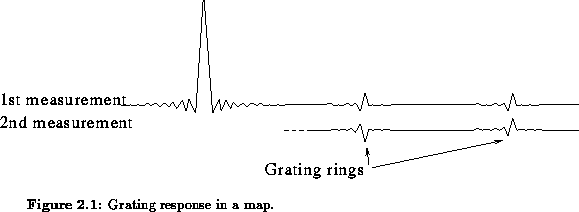Thus, to minimize the disturbances caused by the grating rings, the steps (in wavelengths) between the measured circular tracks in the plane should be small. Figure 2.1 shows a cross-section of the synthesized pattern including the first two grating rings. Adding a second measurement with the movable antennas shifted by 26 m will give a regular spacing of 36 m between the circles in the plane. This corresponds to grating rings with twice the previous radii, i.e. all the odd-numbered rings have been eliminated. After 2, 4, etc. measurements with suitable positions of the movable antennas, the remaining grating rings will be 2, 4, etc. times as in the original set of rings. A general treatment of grating rings is given by Bracewell and Thompson (1973).

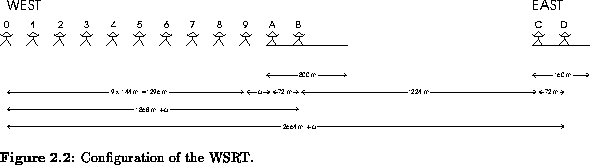
Since 1990 the WSRT can work in a new observing mode, using the mosaicing technique. Recent on-line and off-line software development by R. Braun, H. van Someren-Gréve and W. Brouw has made this mosaicing concept possible and allows us to make this mosaicing concept more understandable in terms of theoretical knowledge and software implementation. Because of these developments it allows us to make this survey possible. This is the only way at this moment to observe large areas of sky in one 12 hour observation.