Relativistic beaming

In this paragraph one of the consequences of the theory of relativity is examined in more detail. It is about the difference of the radiation pattern of particles when they have highly relativistic speed. It follows the discussion of Rybicki and Lightman (1979).

The special theory of relativity is based on two postulates:

1. The laws of nature are the same in two frames of reference in uniform relative motion with no rotation.
2. The speed of light is in all such frames.

Consider two frames and (see figure 11) with a relative uniform velocity along the axis. The origins are asumed to coincide at . If a pulse of light is emitted at the origin at , each observer will see an expanding sphere centered on his own origin. This is a consequence of postulate 2 and is inconsistent with classical concepts, which would have the sphere always centered on a point at rest in the "ether". We cannot review time and space separate, because they are both connected in each observer-frame. Therefore, we have the equations of the expanding sphere in each frame:

where does not equal , as in Newtonian physics. Instead of the Galileo transformation we will have to use the Lorentz transformation, which gives the actual relations between and :

where

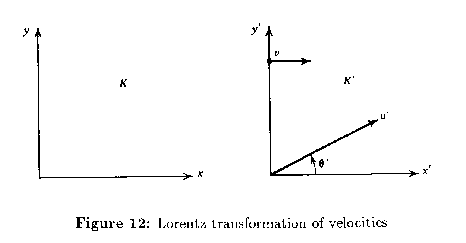
One of the consequences of the Lorentz transformation has to do with the transformation of velocities. If a point has velocity in frame , what is its velocity in frame (see figure 12). Write the Lorentz transformation in differential form:

We then have the relations

The generalization of these equations to an arbitrary velocity , not necessarily along the axis, can be stated in terms of the components of perpendicular to and parallel to :

The directions of the velocities in the two frames are related by the aberration formula

where .

An interesting application is for the case , where

These equations represent the aberration of light. Suppose a photon is emitted at right angles to in (). Then we have

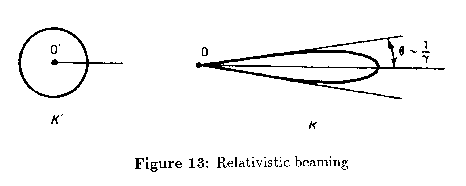
Now for highly relativistic speeds, becomes small:

If photons are emitted isotropically in , then half will have and half (see figure 13). Equation (30) shows that in frame photons are concentrated in the forward direction, with half of them lying within a cone of half-angle . Very few photons will be emitted having . This is called the beaming effect.