Modelling the central engine

This discussion follows the calculations made by Moffet (1975). What we would like to have is an estimate of the energy requirements for a radio source. This is possible for synchrotron sources if we know the luminosity, the spectral distribution of the emission and the intensity of the magnetic field. The luminosity can be determined if you know the distance and this value can be obtained from a redshift measurement (usually calculated from optical spectroscopy data). You can calculate the spectral distribution directly from radio flux measurements. The only parameter you cannot measure directly is the magnetic field.

This section deals with the assumptions and calculations you have to make to get a working model. Lets say that the source consists of a volume . In this volume there is a tangled magnetic field with average strength . We also have electrons in this field with average density between energies and . The electron energy density can be written as

The total electron energy . Now let . Then

How can we calculate in terms of the luminosity and the magnetic field? For one electron, the rate of emission (summed over all frequencies) is given by

In this formula we neglect the geometric factors and assume an average effective magnetic field equal to . The total luminosity of the source can be calculated by integrating over the electron spectrum

Doing the calculations you find that

. This formula might look awful, but is says that the total electron energy is proportional to times a shape factor which depends on and the energy range.

If you know that there is a cutoff frequency in the radiospectrum, it is better to evaluate the total electron energy in terms of cutoff frequencies and and the spectral index . If we assume that each electron only radiates at its critical frequency (the frequency near which the emission is a maximum) we may use

(comes from synchrotron emission frequency). This changes the formula of the total energy in electrons as follows:

The electron energy now depends on and on a shape factor in frequency. For rather flat spectra () an upper cutoff frequency is required to avoid a divergence. For the same reason you need a lower cutoff for steep spectra (). You can use the electron rest-mass energy as a lower cutoff energy, because electrons with these amounts of energy are not relativistic and therefore will not produce synchrotron radiation. Many radio sources show departures from a powerlaw spectrum in the range of ten to a few hundred MHz, and a lower cutoff frequency of Hz is often assumed.

The calculations are based entirely on the properties of electrons, but these are not the only particles that carry energy in these sources. Protons and other heavy particles are also present, but they emit negligible amounts of radiation, because they are accellerated much less by the Lorentz force. Therefore we need to estimate the relative amounts of energy in relativistic electrons and in energetic baryons. This can be done by monitoring the primary cosmic-ray spectrum observed at high altitudes above the Earth. These observations tell us that electrons account for about 2 percent of the energy. Thus if we set the total particle energy , the value of near the Earth is something like 50. Theoretical models give values of about 100 for .

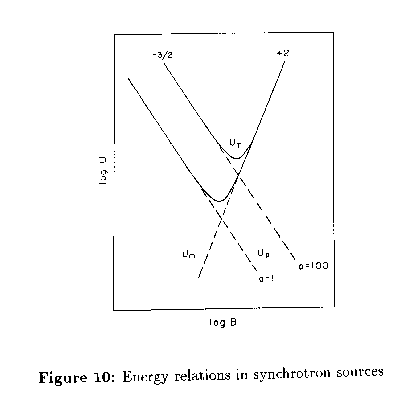
The energy is not only stored in the particles, but also in the magnetic field. The field energy density is equal to , so the total magnetic energy . The total energy of the source is

The energies are shown as functions of in figure 9. The particle energy varies as , so it dominates for small field strengths and the magnetic energy varies as ; thus it dominates when the magnetic field is large. The total energy has a minimum near the value of for which and are equal. We then make the assumption that the magnetic field is actually equal to the equipartition value (because even the minimum energies for radio galaxies are extremely large), which gives the mimimum energy.

Calculate the minimum by using . The minimum energy condition is then

Estimates of will be in error by a factor of 4 even if our guess of the value is in error by an order of magnitude. The estimate is also not sensitive to errors in the measured source dimensions.